Part of creating good topology for subdividable models is to avoid T-vertices (T-verts) in your work. A T-vertex is a convergence of an edge in T formation, and the practice of using T-verts should not be used unless it is absolutely necessary for the flow of a model’s shape. If you use T-verts incorrectly, they will halt edge flow of your model and cause poor subdivision.
You should consider any vertex with only three edges to be a T-vertex even if the crossbar of the T is not a horizontal line. You can use T-Verts when there’s no better solution, but it is best to avoid them as much as possible. Below, we’ll look at both acceptable and unacceptable T-vert uses.
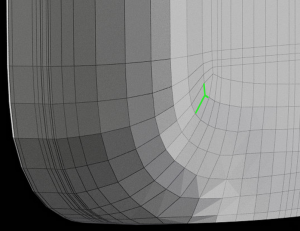
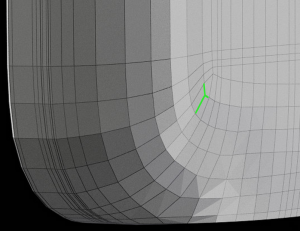
Acceptable T-vertex

Unacceptable T-vertex
Flowing Around Corners – Acceptable
It is necessary to use T-verts when the quad flow from one direction meets the quad flow from another direction.
On this rabbit model, an acceptable T-vertex forms where the edge flow up the side of the ear meets the edge flow across the top of the ear.
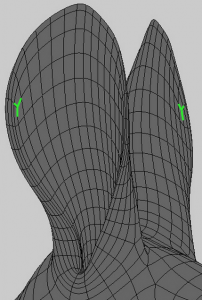
Clean Edge Flow
On cell phones and other electronics, an acceptable T-vertex forms when the quad flow from the side of the phone forms a corner with the flow across the bottom of the phone.
Clean Edge Flow
Insets – Acceptable
Creating extra detail by using Oblong Cutouts will create T-verts. In this case, these vertices are acceptable as this method is the best way to increase detail within a specific area while still maintaining edge loops that are easily selectable.
Using the recommended method for increasing detail creates acceptable T-vertices.

This type of construction is easy to edit and results in easily selectable edge loops.
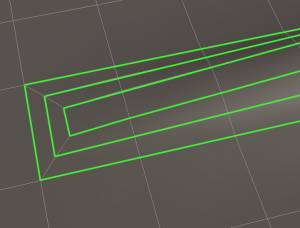
You (or the customer) can easily select rings of edges…

…and create a new set of edges by connecting the ring selection.

Transitioning with Other Methods – Usually Unacceptable
Artists sometimes use T-verts as a solution to transitioning an area of higher detail to an area of lower detail. This method is acceptable as long as your transition uses insets as described above. A straight T crossbar often indicates poorly planned topology.
A T-vertex with a straight crossbar is usually not the best solution.

It’s better to extend the edges…

…or make the sleeve and arm separate objects…

…or rearrange the edges so that you can use insets.

To create quality topology, you should use insets. However, be sure that your insets are necessary, meaning that there is no other way to create the topology. Sometimes using insets can result in extra edges (see model below). Without unnecessary edges, the model keeps its exact shape, so it is optimal for you to remove those edges.
Unnecessary Use of Inset Method – Unacceptable
Although the T-vertices (yellow) are created with an inset structure, the red edges are unnecessary for this object and should be removed altogether.

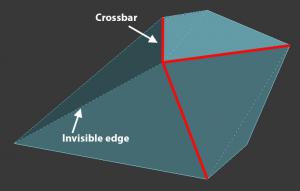
Bent Polygon – Unacceptable
A bent polygon can result when you use T-vertices that cause polygons to bend along a hidden edge that flows from the supporting bar of the T. Using bent polygons results in substandard topology that will create undesirable effects in renderings.
Poorly planned T-vertices can result in a bent polygon that causes abnormalities in topology.
In this case, you would add an edge should in place of the hidden edge. You would then adjust the resulting topology to create good edge flow.
These are just guidelines for T-vertices. As with all of your topology, you should be constantly asking yourself, “Is there any way this could be better?” The existence of T-vertices in any situation other than the first two listed here is usually a sign that your topology could be (and should be) better.




